Conspect al capitolului 4, ”Graphic representation of frequency distributions”, din ”Statistical reasoning in psychology and education”, de Minium, King și Bear.
Prezentarea sub forma unui grafic poate să faciliteze identificarea anumitor caracteristici ale datelor.
Distribuțiile de frecvență pot fi prezentate sub formă de histogramă, poligon de frecvență și curbă de procentaje cumulative. Ilustrarea grafică se poate găsi la paginile 51, 52 și, respectiv 59.
Proceduri fundamentale
Graficele distribuțiilor de frecvență au două axe: una orizontală și una verticală. Cea orizontală se numește abscisa sau axa X, iar cea verticală este ordonata sau axa Y. Se obișnuiește să se reprezinte scorurile sau categoriile pe axa orizontală, iar frecvențele pe axa verticală.
Histograma
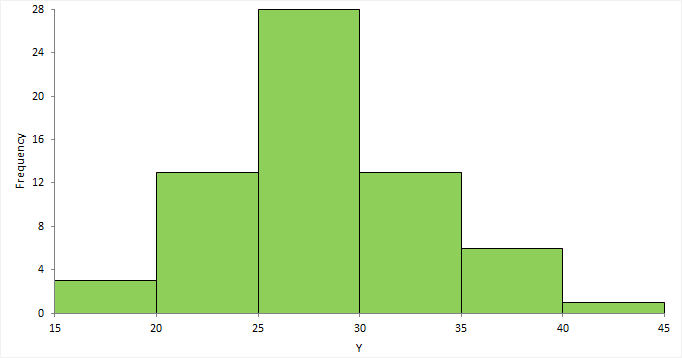
Histogramele sunt reprezentate de o serie de dreptunghiuri, câte unul pentru fiecare categorie sau scor. Înălțimea dreptunghiului – și deci valoarea pe axa Y – este dată de frecvența acelei categorii sau acelui scor.
Construirea unei histograme pornește de la tabelul de frecvențe sau de la afișarea tip tulpină-frunză (stem-and-leaf). Fiecare bară sau dreptunghi va corespunde frecvenței unui scor, clasă sau interval. Nu ar trebui să existe spații goale între intervale, cu excepția categoriilor care au frecvență 0.
Poligonul frecvențelor
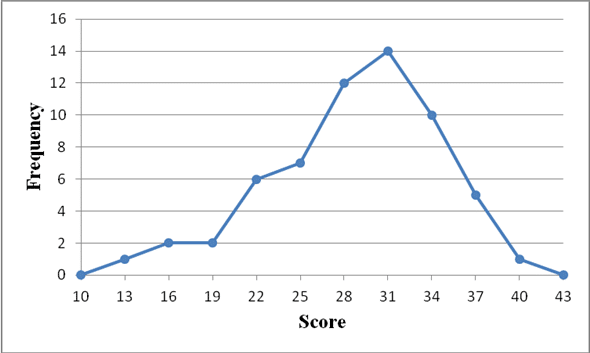
Poligonul de frecvență reprezintă o serie de puncte care sunt conectate între ele. Fiecare punct corespunde unui scor, clasă sau interval și este poziționat mai sus sau mai jos în grafic, în funcție de frecvență.
Cum alegi între histogramă și poligonul frecvențelor
Histogramele sunt utilizate când ilustrăm o distribuție de frecvență negrupată a unei variabile individuale. Dacă variabila nu este continuă, histograma transmite implicit că nu există alte scoruri între cele prezentate pe axa orizontală.
De asemenea, ea este preferabilă când prezinți frecvențe relative. Aria fiecărui dreptunghi este o fracțiune din aria totală a histogramei la fel cum frecvența acelei clase este din numărul total de cazuri din distribuție.
Poligonul este preferabil pentru distribuțiile de frecvență grupate. Dacă există o tendință de creștere sau descreștere a frecvenței de-a lungul mai multor intervale consecutive, poligonul va reprezenta această tendință mai direct. Din acest motiv, dar și pentru că sugerează mai bine continuitatea, poligonul frecvențelor este preferabil pentru a etala distribuția unei variabile continue.
Poligoanele de frecvență sunt mai utile când comparăm două sau mai multe distribuții.
Diagrama de bare și diagrama circulară (”plăcinta”)
Când trebuie să exprimăm grafic date categoriale, avem la dispoziție diagrama de bare și diagrama circulară.
Diagrama de bare este foarte similară histogramei, doar că apar spații între dreptunghiuri, sugerând discontinuitatea inerentă categoriilor discrete, cum este cazul răspunsurilor prin ”da” sau ”nu”. Acest tip de diagramă poate fi folosit pentru a etala subcategorii din cadrul unei categorii. În această situație, barele sunt adiacente.
Spre deosebire de diagrama de bare, unde pot fi afișate atât frecvențe brute, cât și relative, în diagrama circulară sunt reprezentate exclusiv frecvențe relative, unde suma lor trebuie să fie 100.
Curba procentajului cumulativ
Un procentaj cumulativ indică procentul de scoruri care se află sub limita superioară a clasei reprezentate. Prin urmare, în construirea curbelor de procentaj cumulativ, acesta este reprezentat relativ la limitele superioare reale ale fiecărui interval de pe axa orizontală.
Odată reprezentate grafic procentele pentru limita superioară a fiecărei clase, punctele obținute sunt conectate printr-o linie dreaptă.
O curbă de procentaj cumulativ nu poate să aibă o pantă descendentă. Întotdeauna evoluează crescător (pentru că este cumulativă). Când o clasă nu conține nici un scor, linia se menține orizontală.
Factori care afectează forma graficelor
Nu există un singur grafic pentru un set de date. Același set de date brute poate fi grupat în modalități diferite, iar aspectul graficului se va modifica în consecință.
Și mai importantă este problema scalării relative. Frecvențele și scorurile sunt unități diferite. Nici un principiu nu specifică numărul echivalent din fiecare.
De asemenea, graficul poate să fie diferit în funcție de scala de măsurare folosită pentru frecvență.
Frecvența pe axa verticală trebuie să fie întotdeauna continuă de la 0. Dacă segmentezi axa și începi afișarea de la o valoare mai mare, se pierde relația proporțională dintre intervalele de frecvență. Spre exemplu, o categorie de 11 și una de 15 vor părea semnificativ mai diferite dacă începi graficul de la 10, decât dacă îl începi de la 0.
Dacă ne interesează forma distribuției obținute pentru eșantionul nostru, atunci este esențială dimensiunea eșantionului și randomizarea selecție unităților din eșantion. Când avem un număr limitat de scoruri extrase din populație, patternul rezultat poate fi foarte diferit de patternul populației.
Caracteristici ale distribuțiilor de frecvență
Trei caracteristici descriu împreună o distribuție de scoruri: forma, tendința centrală și variabilitatea.
Forma
O distribuție poate să fie normală (clopotul lui Gauss) sau să fie înclinată pozitiv (spre dreapta) sau negativ (spre stânga).
Un alt tip de distribuție este cea rectangulară, în care numărul de scoruri este egal pentru fiecare categorie.
De asemenea, distribuția poate fi bimodală, care sugerează existența a două grupuri cu scoruri care gravitează în jurul a două medii diferite.
Tendința centrală
Unde, pe scala scorurilor posibile este acel punct care reprezintă cel mai bine nivelul general al tuturor scorurilor. Acest punct poate fi reprezentat de medie, dar sunt și alți indicatori ai tendinței centrale.
Variabilitatea
În ce măsură scorurile sunt concentrate în jurul punctului central? Sunt ele adunate sau răsfirate? Acestea sunt întrebări despre variabilitatea sau dispersia scorurilor.
Radu este psiholog, doctor în psihologie, consultant organizațional, antreprenor și editorul fondator al Psihoteca.
